AOS 2 Lecture Screens

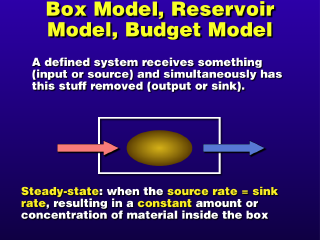
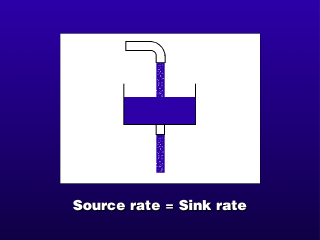
To get dosages and exposures, we need to find the concentration of pollutants in the atmosphere. We define a specific volume---the box---in which pollutants mix. Then we see that sink processes result in a continuous removal of pollutants while emissions are continuous sources of the pollutant. If the source rate is the same as the sink rate, then the concentration of pollutant in the box should remain constant (because the absolute amount of pollutant inside the box is constant when source=sink). This steady-state concentration will be the concentration of pollutant used to determine health effects from a particular source or emission rate.

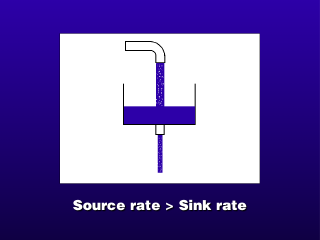
In real-life situations, the sink rate is not necessarily equal to the source rate at any one time, so the concentration will not be steady-state. However, since the absolute sink rate usually has some dependence on the current concentration of the pollutant in the box (generally, the higher the concentration, the higher the absolute sink rate), there may be a natural tendency for the concentration to change so that the sink rate changes until it is equal to the source rate, at which point we will achieve equilibrium.

This is an example of a steady-state box system. The basin is being filled with water from a faucet (rate of water flow is the source rate) while water drains out the bottom (rate of water flow here is the sink rate). As long as the rate at which water drains out is the same as the rate water flows in, the level of the water in the basin will remain constant.

This shows a box system where the flow of water in exceeds the flow of water out. This box will not be in steady-state; the level of the water in the basin goes up as time passes. In a real-world situation, the rate of water flow out the drain will be proportional to the level of water in the basin (the pressure from the deepening water forces more water out the drain as the water level rises), so there may be a point where the water flow rate out equals the (constant) inflow rate, at which time the level of the water in the basin becomes constant. This would demonstrate that many natural box or reservoir systems tend to natural gravitate toward a steady-state configuration, which is why the steady-state box model is so important to study.