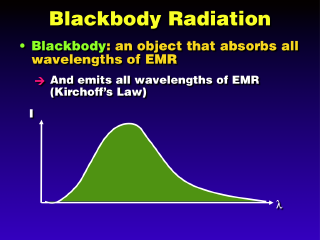
Blackbodies are special objects that have 100% absorption of all wavelengths of EMR. There are few, if any, true blackbodies in nature; however, most objects are pretty close to being blackbodies if we ignore the reflection of visible EMR that allows us to see them.

Kirchoff's Law states that all objects emit radiation as well as they absorb it. So, blackbodies must emit at all wavelengths. There is not uniform emission at every wavelength, however. There will be only one wavelength at which the emission intensity is maximum; this is called lambda-peak or lambda-max. At other wavelengths, particularly the shortest and longest ones, the emission intensity is much lower. Thus, most of the energy emitted by a blackbody is emitted at a few wavelengths around lambda-peak.

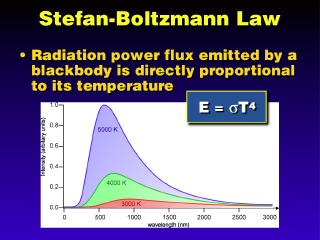The Stefan-Boltzmann Law just states what we already know intuitively: that the hotter an object is, the more energy it radiates out. To be more precise, the power flux (energy per unit time, such as Watts, per unit surface area, such as square meters) is proportional to the fourth power of the temperature (in Kelvin). This fourth power dependency means that the power output goes up very fast for modest increases in temperature. For example, doubling the temperature (T increases to 2T) results in the power output going from T^4 to (2T)^4 = (2^4)(T^4) = 16T^4. The power flux increases by a factor of 16 for a doubling of the temperature (for a tripling of T, the factor becomes 81). The Stefan-Boltzmann Law can also be used to determine radiation temperature from a measured power flux (this is how we determine the Earth's surface temperature from the known strength of the incoming sunlight).

The Inverse-Square Law states that the intensity of the radiation being emitted from some object decreases as the distance from the object increases. It goes down by the square of the distance because radiation is being spread over a sphere surrounding the object, and the surface area of the sphere is proportional to the square of the radius (which is the distance from the object). As radiation energy is spread over an increasing amount of surface area, the intensity goes down proportionally,.

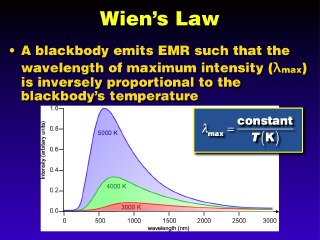Wien's Law says that the value of lambda-peak is inversely proportional to the blackbody's temperature (as the temperature increases, lambda-peak decreases). Looking at blackbodies that have lamda-maxes in the visible range, Wien's Law implies that the warmer objects are more blue (blue is short wavelength visible) and cooler objects are redder (red is long wavelength visible). The constant in the equation is about 3000, if the temperature is in Kelvins and the wavelength is in micrometers. The sun has a radiation temperature of about 6000 K, so lambda-max is around 0.5 micrometers, or the middle of the visible light range. We could also do this in reverse: measure lambda-peak, then get the blackbody radiation temperature. This is how we actually got the sun's surface temperature in the first place, and how we can get the temperatures of objects remotely (note, however, that it's not terribly accurate, since the real surface temperature of the sun is more like 20,000 to 30,000 or more Kelvins).

So, by Wien's Law, we see that the Sun emits mostly visible radiation because its blackbody temperature 6000 K corresponds to lambda-max in the middle of the visible spectrum. The Earth is much cooler, since the sunlight that heats it is much less intense than it is at the surface of the Sun, so its lambda-max is in the infrared spectrum. The fact that these two types of radiation are much different is the reason the atmospheric greenhouse effect works, since the Earth's atmosphere is not a blackbody at all; rather, it transmits visible radiation (i.e., sunlight is not absorbed by atmospheric gases) while infrared radiation is absorbed by the atmosphere.